|
Caña de Azúcar, Vol. 11 N° 2. 1993. DETERMINACIÓN DEL ÁREA FOLlAR EN PLANTAS DE CAÑA DE AZÚCAR VARIEDAD C 323-68 Franky Méndez* *FONAIAP-CENIAP (AGROCLIMATOLOGIA). |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
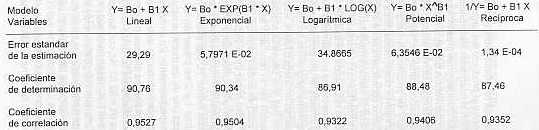
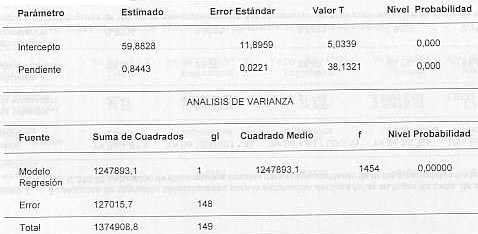
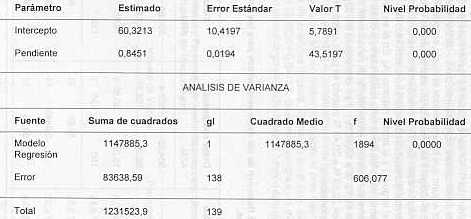
RESUMEN Este trabajo consistió en estimar el área foliar en caña de azúcar variedad C 323-68 a través de mediciones lineales, hechas sobre 150 muestras foliares. Análisis de correlación y regresión fueron usados en éste estudio, para determinar la mejor ecuación en predecir el área foliar en caña de azúcar variedad C 323-68. Diferentes métodos estadísticos fueron utilizados a fin de encontrar el mejor ajuste, correspondiendo éste al modelo lineal (y = bo + b1 X). Palabras clave: Saccharum spp., área foliar, dimensiones lineales. INTRODUCCIÓN El área foliar es uno de los parámetros más importantes en la evaluación del crecimiento de las plantas; de allí que la determinación adecuada de la misma sea fundamental, para la correcta interpretación de los procesos en una especie vegetal. Existen diferentes métodos para la determinación del área foliar. Su selección en un momento dado, dependerá del objetivo para la cual se realiza la medición y del nivel de precisión deseado en el trabajo. El tamaño de la muestra, la morfología de la hoja y las disponibilidades de tiempo y equipo, por parte del investigador, son aspectos de importancia relevante en la escogencia del método a emplear. Cuando las plantas son individualizables, las medidas lineales de la hoja pueden utilizarse en relaciones matemáticas simples; en caso de hojas muy grandes como las de banano, caña de azúcar o maíz, generalmente se determina el área como el producto del largo por el ancho. Cuando se trabaja en análisis, con fines de vegetación, cambios de biomasa y en general cuando se utilizan grandes poblaciones de plantas no individualizables, lo más conveniente es determinar el área foliar de las plantas utilizando una sub-muestra representativa de la población, sistema este que también se puede aplicar en la determinación del área foliar en la copa de un árbol. El área foliar ha sido objeto de interés en los estudios de fisiología vegetal y gen ética, ya que se encuentra muy relacionada con la eficiencia fotosintética de los cultivos (1, 8, 9, 12) y es por esto que se requieren procedimientos sencillos y rápidos para realizar la evaluación. Se han desarrollado diferentes métodos para la planimetría, la aplicación de ecuaciones y coeficientes, etc; para diversos cultivos, entre ellos la caña de azúcar (1, 5, 6) de gran importancia comercial por el área que ocupan en la agricultura cañera mundial. Kemp.(6), en investigaciones realizadas sobre diferentes tipos de pasturas y otras especies encontró diferentes ecuaciones de regresión, las cuales fueron examinadas considerando el peso de las hojas para lograr de manera satisfactoria la constante de la ecuación (K), en el modelo A= KLB, donde L= longitud de la hoja en cm, B= el punto mas ancho de la hoja en toda su longitud en cm, A = área en cm2. Un conjunto de 4 variedades de pasturas fueron examinadas y la ecuación A= 0.905 LxB fue la más consistente en todo el conjunto de datos analizados. Gómez et al. (4), realizaron estudios de los coeficientes para el cálculo del área foliar de algunas variedades de caña de azúcar. En muestras sucesivas tomaron 780 láminas de hojas de la variedad C. 43972, de cualquier edad e inserción en la planta, midiendo a las hojas el largo y el ancho máximo. Posteriormente determinaron el área foliar de cada una de las hojas con un medidor electrónico, calculando el coeficiente según la siguiente relación: C = Área foliar real/(LxA). donde: L: es el largo de la hoja, en cm. El coeficiente resultó igual a 0.75 para el área foliar de la variedad en cada ciclo, o etapa fenológica. San José y Medina. (13), en un análisis de productividad en caña de azúcar, variedad PR 980, sembrada en Tacarigua estado Carabobo, determinaron la superficie foliar con un planímetro fotoeléctrico a lo largo de todo el ciclo del cultivo. El incremento del índice de superficie foliar (m de hoja/m de suelo) fue casi lineal hasta los 230-250 días, encontrando que la producción de hojas balanceo la perdida por muerte de las hojas basa les del cañaveral. Caruso et al. (3), encontraron dentro del estudio de los índices biométricos de dos variedades de caña de azúcar, que el aumento del área foliar mantenía un comportamiento semejante. En ambas variedades el lAF máximo fue de aproximadamente 3.7 correspondiente a 410 dm2 de área foliar por planta, lo cual se encontraba dentro de los limites citados en la bibliografía. Así mismo, el índice de área foliar aumentó continuamente hasta el máximo de 3.7 dm2 logrado a los 300 días después de la siembra, permaneciendo casi constante hasta el final del ciclo del cultivo. La razón por la cual se ha considerado la variedad C 323-68 en el presente estudio, obedece a su alto potencial de producción como resultado de las evaluaciones en ensayos regionales (16), y su alta aceptabilidad por la agroindustria. Es así que debido a la importancia que tiene la evaluación de diferentes cultivares cañeros, se plantea la necesidad de determinar el área foliar para la variedad señalada, lo que facilitará una mejor interpretación de los resultados de las investigaciones en las que éste cultivar pueda estar involucrado. MATERIALES Y MÉTODOS Se usó la variedad de caña de azúcar C 323-68, tomándose las muestras en un tablón con 3 años de producción comercial (soca 2). El campo de producción está ubicado a unos 20 Km. al noreste de la ciudad de Maracay , en la Región Central del país, con coordenadas aproximadas de 10° 17' LN y 67° 37' LO, en un suelo franco-arcilloso, perteneciente a la serie Maracay. (orden Mollisol). Clasificación climática según Holdridge de bosque húmedo pre-montano subhúmedo. Se tomaron 150 muestras de láminas foliares de diferentes lugares de inserción en la planta, a las cuales se les midió el área foliar, haciendo uso de un integrador de áreas electrónico, marca Licor modelo 30100, con una precisión de 0.10 cm2. Posteriormente, a cada una de las láminas foliares se les midió el largo (L) en cm, y el ancho máximo (A) en cm. Para el presente caso, los datos se agruparon en pares de datos para su posterior procesamiento. Primer par de datos: largo en cm (L) contra el área medida por integrador electrónico en cm2 (AFM), segundo: ancho máximo en cm (A), contra (AFM). El tercer y último par conformado por el producto entre (L) y (A) en cm2, contra (AFM). Los métodos utilizados ampliamente en la determinación del área foliar se encuentran, detallados y discutidos por Sestak, et al. (14). El método estadístico empleado fue el de regresión lineal simple bajo 5 diferentes modelos: lineal, de potencia, exponencial, logarítmico y recíproco, éste análisis se hizo haciendo uso del programa statgraphics, versión 5.0. RESULTADOS Y DISCUSIÓN El análisis consistió en correlacionar el valor de área foliar obtenida por el integrador electrónico (AFM) en cm, con el largo (L) en cm, el ancho máximo (A) en cm, en las posibles combinaciones entre ellos, haciendo uso del método de regresión lineal simple, para cada uno de los modelos señalados anteriormente, lo que representa 150 pares de datos, agrupados según los parámetros largo (L), ancho máximo (A) y área foliar medida por el integrador electrónico (AFM). De acuerdo a los resultados obtenidos se optó por dejar solamente el análisis hecho entre el producto del largo (l) por el ancho máximo (A) y el área medida con el integrador electrónico (AFM), esto como consecuencia de las bajas correlaciones presentadas en los 5 modelos estudiados para los 2 agrupamientos de datos restantes. En el análisis de regresión se encontraron datos que según Barnett y lewis (2) son conocidos como los "outliers" que no son otra cosa que aquellos puntos que se encuentran fuera de la línea de intervalos de confianza para los valores observados (línea segmentada externa en los gráficos 1 y 2). Como consecuencia de esto, se procedió a realizar el análisis para los pares de datos completos (150), y para los pares de datos reducidos (139). En total fueron 11 pares de puntos que fueron eliminados una vez obtenidos los resultados del análisis de regresión. De acuerdo a las consideraciones descritas por Barnett y lewis (2), en una muestra de tamaño moderado tomada de una población, aparecen uno o más valores que son sorprendentemente grandes con respecto a la media del grupo. Esos aparentes valores erróneos o falsos, aunque la población tenga una distribución normal, hay una pequeña posibilidad de que ocurran en el experimento y pueden ser el resultado de una medida o trascripción errónea, en cuyo caso se deben rechazar. Sin embargo si ese no es el caso, los "outliers" pueden ser observaciones genuinas, altamente significativas y sugerentes, a las cuales debe proporcionárseles considerable atención ya que suministran información muy importante. En este caso los "outliers" que en total fueron 11, representan el 7.3% de la población. En los cuadros 1 y 2 se presentan los resultados del análisis de regresión, para cada uno de los modelos estudiados: datos completos y datos reducidos respectivamente. En ambos cuadros se puede apreciar que se encontraron coeficientes de determinación altamente significativos para casi todos los ajustes efectuados, siendo el modelo lineal, el que mayor ajuste proporcionó para los datos completos (R = 90.76 %) y para los datos reducidos (R = 92.82 %), con funciones y = 59,88 + 0,8443 X y y = 60,32 + 8,8451 X, respectivamente. En ambas ecuaciones X representa el producto entre largo (L) en cm y el ancho máximo (A) en cm, para cualquier etapa fenológica del cultivar, con lo que se puede evidenciar que con la eliminación de los "outliers" se mejoró el ajuste en todos los modelos analizados. En los cuadros 3 y 4 se señalan los análisis estadísticos y de varianza para el modelo lineal, haciendo uso de los datos completos y los datos reducidos. En ambos casos se puede señalar que para el nivel de significación del 1 % las ecuaciones generadas por el modelo son altamente significativas, no existiendo dentro de los niveles de probabilidad, valor alguno que hiciera reducir el ajuste encontrado.
En el cuadro 5 se presenta un resumen de los valores de la media (X), desviación estándar (S), y coeficiente de variación para los datos de área foliar real, generados por integrador electrónico de áreas y el producto entre el largo (L) y el ancho máximo (A). En él se puede apreciar un comportamiento de los datos cuya tendencia es a disminuir la dispersión de los mismos al reducirse el coeficiente de variación en los datos del integrador de 19,05 % a 18,65 % , y en el producto del largo por el ancho máximo de 20,59 % a 20,45 % cuando se pasó de los datos completos a los datos reducidos.
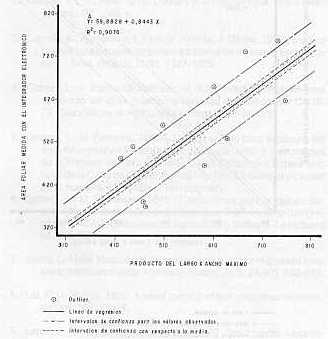
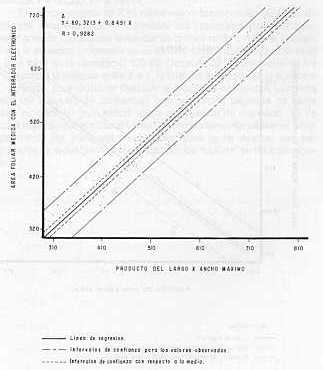
El análisis de la relación entre las medidas lineales y el área real de las hojas en la variedad C 323-68, indican homogeneidad dentro del cultivar seleccionado. En el cuadro 6 se pueden observar los diferentes tamaños de muestras de las hojas de la variedad estudiada, concebidos de acuerdo al ancho máximo y que va desde 3,0 hasta 5,4 cm. como valores extremos de ese parámetro. Se puede apreciar que el 86 % de las láminas foliares analizadas se encuentran entre 3,54,9 cm de anchos máximos, lo que se traduce en que dicha variedad se encuentra en una escala intermedia para esos parámetros (11). En la figura 1, se indica el comportamiento de los datos analizados, así como su respectiva función matemática entre el área foliar real y el producto de las dimensiones lineales. El modelo lineal está expresado por la función y = 59,8828 + 0,8443 X; en donde X vendrá a ser expresada como el producto entre el largo y el ancho máximo, función ésta que refleja el comportamiento de los datos completos. Además se pueden apreciar los "outliers" que son los puntos encerrados con un círculo, los cuales están fuera del rango de los intervalos de confianza para los valores observados, representada por línea segmentada más externa con respecto a la línea de regresión. En la figura 2, se muestra el comportamiento para los datos reducidos, en donde el modelo lineal esta expresado por la función V = 60,3213 + 0,8451X.
El efecto marginal de X es disminuido y la proporción de variación explicada esta reducida. Inicialmente los residuales parecen estar aleatoriamente distribuidos alrededor de la línea recta con E= 0, indicando que la ecuación propuesta es un modelo satisfactorio para el análisis de área foliar en la variedad C 323-68. Después de la eliminación de los datos cambia la relación entre X e V, la cual fue explicada en la ecuación de regresión. Es importante destacar que cuando hay puntos extremos (fuera del intervalo de confianza), una proporción pequeña de éstos puede producir un gran efecto sobre la ecuación de regresión. Es de mucha importancia el conocimiento del comportamiento esperado en el experimento por parte del investigador, para poder evaluar que tan importante es el desbalance producido por los "outliers" en las estimaciones.
DETERMINATION OF THE LEAF
AREA IN SUGAR CANE VARIETY ABSTRACT This paper is concerned only with estimates of leaf area obtained from linear measurements of 150 samples. Correlation and regresion analysis were used in order to determine the most suitable equations for predicting leaf area in sugar cane variety C 323-68. Diferent statiscts methods were used to find the most profitable equation to determine the leaf area, corresponding a linear regresion. (y = bo + b1 X). Key words: Saccharum spp., leaf area, linear measurements. BIBLIOGRAFÍA 1. Ackley, W. ; P. Grandall; T. Russell. 1958. The use of lineal measurements in estimating leaf área Proc. Amer. Soc. Horticult. Sci. 72: 326 -330 2. Barnett, V.; T. Lewis. 1978. Outliers in statistical data. John Wiley & Sons. NY., 365 p. 3. Caruso, E.; A. Pereira; I. Fahl; V. Arruda; J. Cione. 1982. Índices biométricos de duas variedades de cana de azúcar. Pesq. Agropec. Bras. (Brasil) 17(9): 1323-1329. 4. Gómez, L.; F. Pardo; G. Ramírez; M. Julia 1987. Coeficiente para el calculo de área foliar en la variedad caña de azúcar C 43972. Ciencias de la Agricultura (Cuba). 31: 124-125. 5. Gómez, L.; M. Ramírez. 1984a. Método simple para el cálculo del área foliar de la variedad de caña de azúcar Ja 60-5. Resúmenes de la Primera Jornada Científica de las Estaciones Experimentales de la Caña de Azúcar de Pinar del Río, La Habana y Ciudad de la Habana, La Habana. (sin paginar). 6. Gómez, L.; M. Ramírez. 1984b. Coeficientes para el cálculo del área foliar de la variedad caña de azúcar C 87 -51. 44to Congreso de la A T AC, Divisiones de Agricultura y Biología, La Habana pp. 292-296. 7. Kemp, C.1969. Methods of estimating the Leal area of grasses from linear measurements. Annals of Botany, N.S. 24(96): 492-499. 8. Lai, K; M. Subba. 1965. A rapid method of leaf area determination. Nature, 167: 72-74. 9. Lerch, G; R. Reyes; R. García; P. leal. 1977. Crecimiento, desarrollo y variación del índice refractométrico (Brix) en seis variedades destacadas de caña de azúcar. Ciencias de la Agricultura 1: 78-105. 10.Meyer, 1.1975. Data analysis for scientists and engineers. Nueva York, Willey. 513 p. 11. Rodríguez, O; V. González. 1984. Caracterización de variedades de caña de azúcar. Rev. Caña de Azúcar 2(2): 89-108. 12.Saini, A.; R. Nanda, 1983. Observations on dry matter production and green leaf area during pre-flowering period in wheat crop. J. Plant Physiol. 26(4): 353-358. 13.San José, J.; E. Medina. 1970. Análisis de la productividad de caña de azúcar. I. Crecimiento, desarrollo de la superficie foliary contenido de clorofila de caña de azúcar "PR 980". Turrialba 20(2): 143-152. 14.Sestak, Z.; J. Catsky; P. Jarvis. 1971. Plant photosynthetic production. La Haya. Junk. 818p. 15.Sokal, R.; J. Rohlf.1969. Biometry. San Francisco. (USA). Freeman. 776p. 16.Uzcategui, C.; J. Bastardo. 1988. Evaluación de variedades de caña de azúcar en el Valle de Aragua. Periodo 1985-1989. Rev. Caña de Azúcar. 6(2): 75-104. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||